Ecuaciones de segundo grado
Introducción historica
Las primeras apariciones
en textos antiguos de “ecuaciones” datan del 1800 al 1600 a.C. en Mesopotamia,
y traen algunos métodos para resolver ecuaciones lineales, aun que claro, la
notación y forma de resolución de antaño dista una infinidad de la que nosotros
poseemos actualmente.
Desde el siglo XVII a.c
los matematicos de Mesopotamia y babilonia ya sabían resolver ecuaciones de
primero y segundo grado. En el siglo XVI a.c los egipcios desarrollaron un
algebra muy elemental que usaron para resolver problemas muy cotidianos que tenían
que ver con el reparto de cosechas y de materiales.
Habrían de
pasar unos cuantos años, hasta el 1650 a. C. , que es la fecha de la que data
el Papiro de Rindh,
escrito en Egipto. En este texto casi puramente matemático se
muestra un método de resolución general de ecuaciones de primer grado. La humanidad acaba de
dar un paso, el primero, para dar la solución general de una ecuación para
cualquier grado. Este papiro muestra además que los egipcios podía
resolver cierto tipo de ecuaciones de segundo grado, aunque aun desconocían un
método general de resolución, que será el siguiente paso de nuestra historia.Pasarían nada menos que 1500 años, hasta que un griego, Diofanto de Alejandría, diera con la fórmula que resuelve casi todas las ecuaciones de segundo grado( la formula que se encuentra arriba), además introdujo un simbolismo algebraico muy elemental al designar la incognita con un signo que es la primera silaba de la palabra griega arithmos que significa numero.
Entonces a la formula de
Diofanto de Alejandria se le llamo formula general , porque como ya se menciono
anteriormente, sirve para resolver casi todoas las ecuaciones de segundo grado,
y caracteriza asi: donde x representa la variable y, a, b y c
son constantes; a es un coeficiente cuadrático (distinto de 0), b
el coeficiente lineal y c es el término independiente.
aunque el
método de Diofanto sólo proporcionaba una de las soluciones, aun en el caso de
que las dos soluciones sean positivas, mas tarde el matemático judeo español Abraham BarHiyya, en su Liber embadorum, discute la solución de estas
ecuaciones. Y después la introdujo a Europa.Explicación sobre la obtención de la formula general
Esta formula se puede emplear en situaciones, tales como la que se muestra en el siguiente problema:
Toño realizó un viaje de 4 horas para visitar a su novia Pamela. Recorrió 126 km en motocicleta y 230 km en automóvil.
La velocidad en el auto fue 8km/h mayor que en la motocicleta. Determina la velocidad y el tiempo en cada vehiculo
A continuación acomodaremos la informacion de forma que sea más fácil el entender que es lo que nos estan pidiendo.
Ya tenemos las cantidades desconocidas y las expresiones con las que las podemos resolver
Es de suma importancia agregar información complementaria ya que pueden ayudar a la hora de plantear la ecuación
En esta parte, ya tenemos la ecuacion con la que encontraremos la velocidad en la moto (incognita)
Explicacion de la obtención de la ecuación:
Tomamos los tiempos tanto en moto como en vehiculo, los sumamos y lo igualamos a 4, que es el tiempo total del viaje.
Para deshacer la suma de fracciones, aplicamos un método muy sencillo que consiste en multiplicar todo por las velocidades x(x+8) despues de eso, lo demas es afectuar la dicha multiplicación y eliminar terminos semejantes, de ese modo obtenemos la ecuación.
Como resultado tenemos una ecuación de segundo grado, ahora emplearemos la formula general que mencionamos al principio para resolverla.
Aplicación de la formula general para resolver ecuaciones de segundo grado
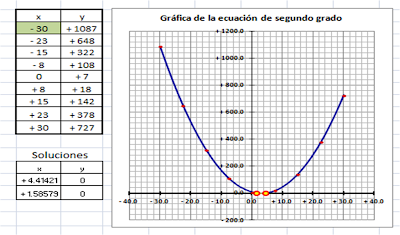
Aplicaremos la formula general para resolver la ecucación que se nos presentó en el resultado del problema.
Al momento de representar el resultado en una gráfica, queda de la siguiente manera.
Ejemplos donde podemos aplicar la formula general:
1.
Gráfica
2.
Gráfica
3.
Gráfica
4.
Gráfica
Gráfica
Otros ejemplos extraidos de libros y paginas de internet, en los cuales támbien los podemos resolver por medio de la formula general
Ejemplos extraidos del libro "Algebra" - Rees,Sparks y de la pag www.profesorenlinea.cl
1.
Ejemplos extraidos del libro "Algebra" - Rees,Sparks y de la pag www.profesorenlinea.cl
1.
Gráfica
2.
Gráfica
3.
Gráfica
4.
Gráfica
5.
Gráfica
En el siguiente enlace podran encontrar el archivo de excel, con el que pudimos resolver las anteriores ecuaciones.














































buen blog cristy :)
ResponderEliminar